Grid fokusering
Fokusering av grid i de laterale retningene
En funksjon som transformerer den uavhengige variable 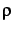 ,
,  ,
til en annen monotont økende avhengig variabel
,
til en annen monotont økende avhengig variabel
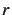 ,
, 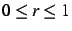 og som samtidig har flekisibilitet til å fokusere grid punkter er den doble
eksponensial funksjonen(Thompson et al., 1999):
og som samtidig har flekisibilitet til å fokusere grid punkter er den doble
eksponensial funksjonen(Thompson et al., 1999):
med parametrene 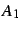 ,
, 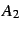 og
og blir gitt av brukeren. Parameteren
blir gitt av brukeren. Parameteren 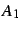 er ønsket verdi av
er ønsket verdi av 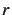 når
når 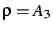 .
.
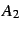 er en strekingsparameter. Denne er brukt til å kontrollere grid
oppløsningen i fokuspunktet. Hvis det normaliserte domenet har
er en strekingsparameter. Denne er brukt til å kontrollere grid
oppløsningen i fokuspunktet. Hvis det normaliserte domenet har
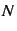 grid punkter blir ligning 1 evaluer i
grid punkter blir ligning 1 evaluer i 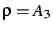 og
og
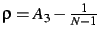 , som representerer nabopunktet.
Differansen mellom disse verdiene av
, som representerer nabopunktet.
Differansen mellom disse verdiene av 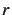 settes deretter lik den ønskede normaliserte oppløsningen
settes deretter lik den ønskede normaliserte oppløsningen
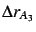 . Dette fører til følgende ikkelineære problem
. Dette fører til følgende ikkelineære problem
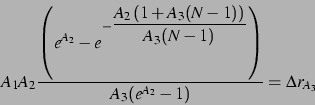 |
(3) |
som løses for 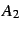 ved hjelp av Newton Rapson iterasjon (Dahlquist and Björk, 1974).
ved hjelp av Newton Rapson iterasjon (Dahlquist and Björk, 1974).
Den siste parameteren i ligning 2, 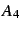 , blir justert automatisk for å sikre kontinuerlig deriverte
når
, blir justert automatisk for å sikre kontinuerlig deriverte
når
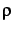 passerer gjennom
passerer gjennom  .
En analytisk ligning for
.
En analytisk ligning for 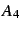 ved å derivere
ligning. 1 og ligning 2 for
ved å derivere
ligning. 1 og ligning 2 for 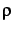 og evaluere i
og evaluere i
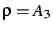 som gir følgende ikkelineære ligning
som gir følgende ikkelineære ligning
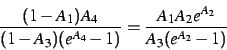 |
(4) |
som blir løst på samme måte som ligning 3.
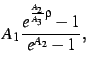
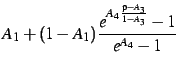
![]() , blir justert automatisk for å sikre kontinuerlig deriverte
når
, blir justert automatisk for å sikre kontinuerlig deriverte
når
![]() passerer gjennom
passerer gjennom ![]() .
En analytisk ligning for
.
En analytisk ligning for ![]() ved å derivere
ligning. 1 og ligning 2 for
ved å derivere
ligning. 1 og ligning 2 for ![]() og evaluere i
og evaluere i
![]() som gir følgende ikkelineære ligning
som gir følgende ikkelineære ligning