Øyvind Thiem, Helge Avlesen og Guttorm Alendal
August 2005

Øyvind Thiem, Helge Avlesen og Guttorm Alendal
August 2005

I området nær Bjorøyna strupes fjorden kraftig inn både i bredde og i dyp. Den vestlige leden kalles Kobbaleia (stiplet blått) og den østlige leden som er hovedleden heter Vatlestraumen (stiplet rødt). I begge ledene er det kjent at kraftige strømmer forekommer, da gjerne på grunn av tidevannsbevegelsene.
19. januar 2004 grunnstøtte MS "Rocknes", en selvlossende bulkcarrier, på et undervannsskjær i nærheten av Revskolten fyr i Vatlestraumen. Skipet begynte raskt å legge seg over og gikk helt rundt på under ett minutt. Av besetningen på 28 omkom 18.
I Kystverkets rapport for "Rocknes"-ulykken , datert 23. november 2004 står dette om området i nærheten av ulykkesstedet:
Vatlestraumen er en del av hovedleden i innseilingen til Bergen sydfra. Farleden mellom Litlesotra og fastlandet på Bergen-siden går i ca 2 nautiske mil rett sørover fra Sotrabroen. Her deler farleden seg i to hvor det ene løpet, Kobbaleia, går sørvestover og det andre, Vatlestraumen, går sørøstover. De fleste større skip velger vanligvis å gå gjennom Vatlestraumen fordi farvannet her i sin helhet er bredere enn Kobbaleia. Løpet gjennom Vatlestraumen er også bedre oppmerket med sektorlys. Men begge løpene er nautisk krevende på grunn av topografien, krav til flere store kursforandringer innenfor et kort tidsrom og den store trafikktetthet i og rundt farvannet av både større og mindre fartøy. I tilegg er strømpåvirkningene sterke og til dels uforutsigbare. I "Den norske los", som gir farvannsbeskrivelser som ikke finnes i sjøkart, fyr og merkelister, beskrives i bind 3a, utgitt av Sjøkartverket, Vatlestraumen slik:
"Vatlestraumen vender tidevannsstrømmen ved HW og LW. Den går N-over med stigende og S-over med fallende vann. På det sterkeste går strømmen flere knop og mange virvler oppstår til sjenanse for mindre fartøyer. Markerte bakevjer under land. Der blir krapp strømsjø når vind og tidevann går motsatt vei."
Strømmen i Vatlestraumen følger ikke alltid sundets retning. Kraftige virvler og stor hastighet på strømmen gjør at det til tider kan være vanskelige forhold. Strømmen kan sette mot Revskolten lykt, kanskje som følge av avbøyninger av overflatestrømmen nord for Hilleren lykt fra landet på nordsiden av Vatlestraumen. Målinger viser at strømmen kan øke i styrke fra overflaten og ned til 5 meter og at overflatestrømmen (ned til 7 meter) har en annen retning enn det strømmen fra 7 meter og dypere har. Vatlestraumen er på nord og østsiden omdekket av fjell og knauser med tett bebyggelse (Hilleren, Kongshaug og Håkonshella). Dette medfører at det ikke er visuelt mulig å se annen trafikk i selve Vatlestraumen før man skal til å endre kursen til den som leder gjennom selve straumen. På sør og vestsiden dvs. Bjorøyna, er lendet skogklett og forholdsvis lavt. På det smaleste av farbart farvann for større skip er Vatlestraumen ca. 220 m bred. Ettersom store fartøy er i konstant svingkondisjon i den ene eller andre retningen når de går gjennom Vatlestraumen, er det uforsvarlig for to større fartøy å møtes her. Derfor er det alminnelig praksis at større fartøy varsler på VHF kanal 16 om tidspunktet de vil passere gjennom Vatlestraumen. Dersom det ligger an til at to eller flere ankommer samtidig, avtaler disse seg i mellom hvem som skal slakke på farten for å unngå en møtesituasjon. I dagslys brukes optiske referanser, så som friseilinger, altså stedlinje som gir trygg passering av en grunne el.. Det er ikke oppgitt friseiling for Revskolten. I mørke har losen støtte i fyrbelysningen for å bestemme sin posisjon i farvannet
Som en forstår er strømmønsteret komplisert i denne delen av seilingsleden til og fra Bergen. Strømmønster og hydrografi påvirker både skipstrafikk og det marine miljøet, og er dermed viktig å forstå.
Når det gjelder å forstå hva som styrer fysiske hendelser i slike områder kan numeriske modeller være til stor hjelp. For å gjenskape et fenomen trenger man riktige startbetingelser og drivkrefter for modellen. Begrenset tilgang på gode drivkrefter er nok den største utfordringen for å oppnå realistiske resultat med numeriske modeller per i dag. Eksempel på fenomen kan være lokale vindforhold som endrer transporten av vannmasser på kort tidsskala, sterke lavtrykk som genererer vannstandsendringer, kraftig nedbør som endrer stratifiseringen i området, eller storskala bevegelser i vannmassene som skyldes lokale fenomener utenfor modellområdet. Bruk av måledata er heller ikke uproblematisk; de er ofte foretatt i et begrenset området eller i en viss tidsperiode. Det stilles også strenge krav til kvaliteten på måledataene.
Vi har i dette forstudiet kun brukt forenklede og idealiserte drivkrefter og initialverdier, basert så langt som mulig på målinger og observasjoner. Vi har ikke studert effekten av vind og storskala dynamikk fra Nordsjøen, men har med en enkel tidevannsmodell og initiell stratifisering som en første tilnærming.
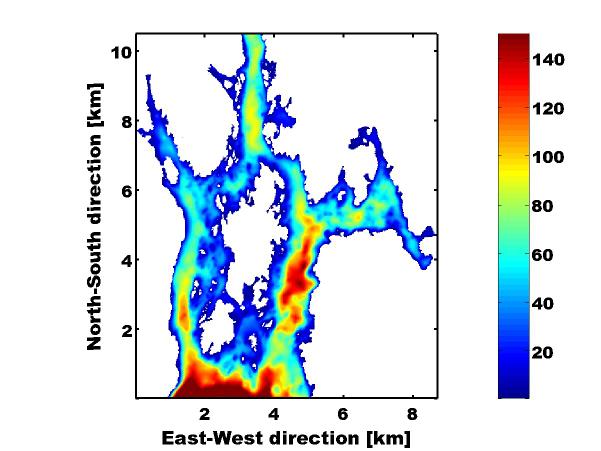
Modellområdet strekker seg fra nordlige Raunefjorden like sør for Tyssøyna til Byfjorden. I sørvest og sørøst er modellområdet avgrenset av Sotra og Flesland. Her er Raunefjorden ca 250 meter dyp på Sotrasiden og ca 100 meter dyp ved Fleslandsiden. Beveger man seg nordover treffer en først på Tyssøyna, så Bjorøyna, de to store øyene som ligger i den nordlige Raunefjorden. Øyene deler fjorden i to. Det vestlige løpet som heter Kobbaleia er grunt med ca 70 meter dyp langs Bjorøyna og en del dypere langs Tyssøyna, hvor det er ca 120 meter på det dypeste. Kobbaleia har et sideløp i nordvest der det er et sund som går mot Bildøy, som ligger mellom Sotra og Lille Sotra. Dette sundet er åpent mot nord gjennom to grunne og trange passasjer som vi har neglisjert og "lukket" i modellområdet. Mot nordøst går Kobbaleia gjennom Steinsundet. Midt i dette sundet ligger det noen mindre øyer, og det er relativt grunt.
På den østre siden av Tyssøyna er dypet rundt 80 meter. Langs den østre siden av Bjorøyna har vi en grop med dyp opp mot 150 meter. Denne blir grunnere der Grimstadfjorden åpner seg i øst. Innerst i Grimstadfjorden ligger Straume der Nordåsvannet renner ut. I modellene er avrenning fra Nordåsvannet ikke tatt med. Videre nordover langs Bjorøyna begynner Vatlestraumen. Vatlestraumen vender mot nordvest og har en terskel som er på rundt 35 meter på det grunneste. Vatlestraumen og Steinsundet møtes på nordsiden av Bjorøyna og går ganske rett nordover til Byfjorden avgrenset på sidene av Lille Sotra og fastlandet. Dypet her er på ca 80 meter.

Figuren viser at den farbare leden for større skip gjennom Vatlestraumen er ca 220 meter bred. Videre ser en at det er relativt langstrakte grunner på Bjorøyna siden, mens det på fastlandssiden er ganske dypt.
Modellen bruker et terrengfølgende kurvelineært koordinatsystem i den vertikale retningen (sigma koordinater), og vanlige "kartesiske" koordinater i de horisontale retningene.
Modell-likningene var opprinnelig basert på antagelsene om hydrostatisk fysikk, men har i de senere år blitt utvidet til også å inkludere ikke-hydrostatiske effekter. Modellen brukes vanligvis i studier med oppløsning på noen titalls km, som ved sokkelkanten, men har med de siste utvidelsene også blitt testet ned på mikroskala nivå med kun få centimeters oppløsning.
I dette studiet har modellen blitt kjørt hydrostatisk. Det vil si at antagelsen om at trykket av en væskesøyle kun er avhengig av vekten av væskesøylen er brukt. Denne antagelsen er ikke helt korrekt siden væskensøylen kan ha en vertikal bevegelse som vil påvirke trykket, men antagelsen reduserer regnetiden betraktelig og er derfor brukt i de fleste havmodeller i dag. For eksperiment hvor den horisontale skalaen er mye større enn den vertikale er dette som regel en svært god tilnærming. I denne simuleringen er den horisontale skalaen av størrelsesorden 10 km, mens den vertikale er noen titalls meter, dvs. mye mindre enn den horisontale.
En annen tilnærming som er gjort er at tetthetsforskjeller blir neglisjert i alle ledd i bevegelsesligningen, bortsett ifra tyngdeleddet. Denne tilnærmelsen er kalt Boussinesq antagelse og er også vanlig å gjøre i havmodeller.
Ligningene som er brukt i BOM finnes i brukermanualen, se http://www.mi.uib.no/BOM. Disse ligningene er i hovedsak likningen for massebevaring, bevegelseslikningene for væske med ovenfornevnte forenklinger, transportlikninger for saltholdighet, temperatur og turbulens, samt en tilstandsligning som beskriver hvordan tettheten kan bli beregnet fra temperatur og saltholdighet.
Det kurvelineære vertikale griddet har den fordelen at koordinatsystemet følger den komplekse bunntopografien, og at man derfor "løser opp", dvs. får tilstrekkelig med grid punkt, til å representere bunn- eller overflatefenomen. Ulempen er at griddet introduserer en numerisk feil i beregningen av trykkgradienter i områder med sterkt skrånende bunn. Disse feilene vil kunne sette opp strømmer som ikke er reelle. Denne svakheten er velkjent, men systemet brukes fortsatt både i atmosfære og havmodeller siden fordelene ser ut til å være større enn ulempene.
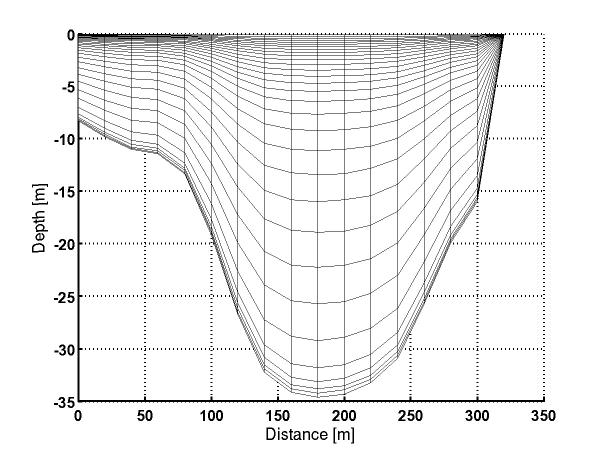
I nordlig og sørlig rand er det brukt FRS soner til å force tidevann. En FRS sone er en del av modellområdet som brukes til å relaksere modell-løsningen mot en ekstern tilstand, i dette tilfellet et tidevannssignal. FRS soner har også sine fordeler og ulemper. De er effektive i og med at de er svært robuste numerisk, og hindrer refleksjoner av støy/numeriske feil som genereres inne i modellområdet og som beveger seg mot rendene. På den annen side er løsningen inne i selve FRS sonen av diverse årsaker ikke fysisk riktig. FRS sonene er i våre eksperiment 7 gridceller brede.
I havet, og turbulente strømninger generelt, foregår det en energioverføring fra lange lengdeskalaer, f.eks. lange bølger eller store virvler, over til kortere lengdeskalaer. En numerisk modell har begrenset romlig oppløsning, dvs. avstanden mellom hvert diskrete punkt i rommet. Dette fører til at modellen ikke kan representere fysikken på så korte lengdeskalaer som fysikken tilsier, og energien som skulle blitt overført til de fineste skalaene må taes ut av modellen på en annen måte. Dette gjøres i de fleste numeriske modeller ved å øke viskositeten, eller regne med noe man kaller Eddy-viskositet. Man kan bruke egne regneverktøy inne i modellen for å estimere denne viskositeten eller man kan sette den eksplisitt. Blir viskositeten for stor blir resultatene urealistisk "glatte" og sirupsaktige, er den for liten kan man risikere numerisk ustabilitet, dvs. at modellen krasjer. Vi har i dette studiet sett litt på effekten av forskjellige nivå for bakgrunnsviskostitet, og fant at man BOM kan bruke 2D viskositet på 0.2m^2/s og 3D viskositet på 0.01m^2/s.
Modellen er ikke diskret bare i rom, men også i tid. En numerisk modell har, hvis den benytter såkalte eksplisitte numeriske skjema begrensinger på hvor store tidsskritt som kan brukes for at det skal gå numerisk stabilt. BOM er en eksplisitt, modesplittet modell. Rent fysisk har den frie havoverflaten en bølgeforplantningshastighet som er mye raskere enn bølgeforplantnings, advektive, og diffusive prosesser i det indre av havet. Siden overflatesignalene kan modelleres til god nøyaktighet med en 2D modell kan vi beregne disse separat med korte tidsskritt, og så beregne de andre prosessene (modene) i 3D med lange tidsskritt. Dette gjør at vi sparer mye beregningstid. I simuleringene beregnes 2D signalene 30 ganger oftere enn 3D signalene, hvert 3D steg er 6 sekunder.
Viskositeten er beregnet ved hjelp av et Smagorinsky skjema, dvs. at viskositeten og diffusiviteten endres lokalt for å ta hensyn til turbulens som ikke blir oppløst. Dette skjer typisk i områder med stort skjær i strømmen. (Stort skjær vil si stor gradient/endring.)
På den nordlige og sørlige randen er det brukt såkalte svamplag. Disse fungerer omtrent likt som FRS-sonene. Hvert av svamplagene er 10 celler brede.
Metoden for fokusering av griddet som er brukt i simuleringene kan en lese mer om her.
Minste gridavstand i senteret av Vatlestraumen er satt til 2.1 meter. Ved rendene blir største gridavstand henholdsvis 279 og 233 meter i Øst-Vest og Nord-Sør retning. For å unngå problemer med FRS sonen ved rendene har 10 grid celler blitt lagt utenpå gridet i nord og sør. I disse grid punktene er dypet satt likt første dyp i det opprinnelige gridet.
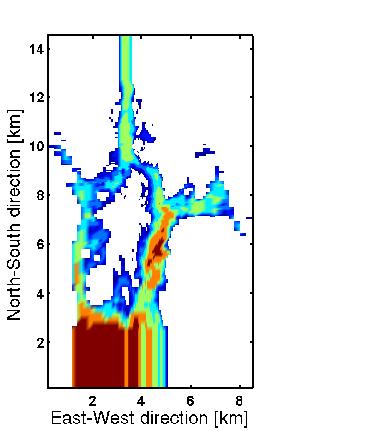
Det har i de senere år dukket opp mange forskningsmodeller som bruker disse teknikkene, men de er ennå lite i bruk operasjonelt. Man slipper nemlig ikke automatisk unna de fundamentale problemene mange finite difference modeller møter. Det kan f.eks. vises at variabel grid-/celle størrelse fører til en redusert numerisk nøyaktighet (orden), som ikke alltid kan oppveies av høyere oppløsning. Irregulære grid vil også ha problem med adveksjon, og må gjerne bruke høyere viskositet enn en tilsvarende finite difference modell for å oppnå numerisk stabilitet. Vi regner med at disse problemene vil bli løst over tid, men foreløpig ser det ut som finite difference modeller holder stand som operasjonelle 3D-modellverktøy. I tidevannsberegning er lineære likninger gode nok approksimasjoner, så der kan det se ut til at finite element modeller dominerer.
I 1973-1974 undersøkte Hans B. Helle fjordsystemene i nærheten av Bergen. På bakgrunn av rapporten hans "Byfjordundersøkelsen 1973-1974. Oseanografisk resipientundersøkelse av fjordene rundt Bergen" (1975) ble en idealisert lineær sjiktning for Raunefjorden satt opp for bruk i modellene. Sjiktningen er laget på bakgrunn av dataene til Helle fra mars 1974 og gitt under.
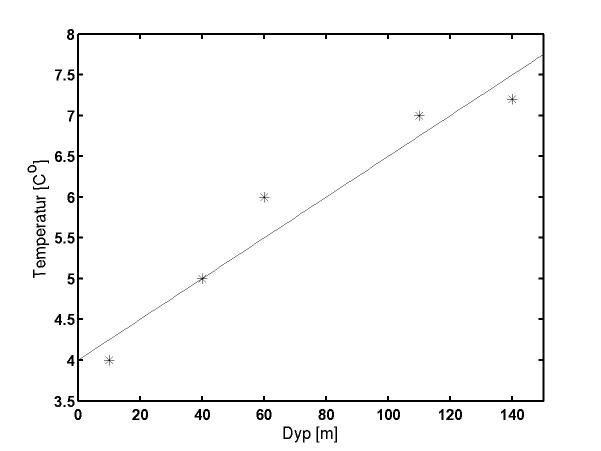

Fra målingene til Helle ser det ut til at isolinjene for temperatur og saltholdighet skråner oppover mot Byfjorden. Dette er ikke tatt hensyn til når sjiktningen ble laget.
Figurene som vises er av dybdemidlede strømhastigheter. Disse er å betrakte som transporten av vannmassene. Maksimal 3D hastighet i modellen vil være høyere, og for simuleringen med lineær sjiktning ligger maksimalverdiene ofte opp mot 0.7 m/s i strømsterke områder. Man må også ha i bakhodet at modell-likningene er de såkalte Reynoldsmidlede likninger, og at hastigheten dermed representerer en middelstrøm også med hensyn på tid.
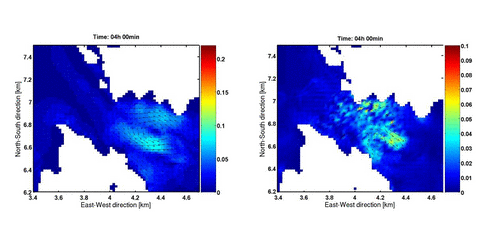
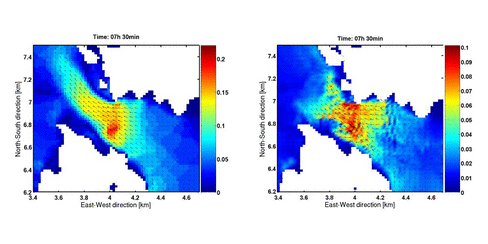
I numerisk fluiddynamikk er viskositet et viktig verktøy for å balansere energien fra lengdeskalaer som modellen ikke løser opp, siden denne energien kan få modellene til å bli numerisk ustabile. Det å velge hvor stor viskositet som skal brukes og hvilken måte den skal beregnes kan være vanskelig. Et eksempel på hvor forskjellige resultater en kan få ser en i figuren under. Eksempelet her er hentet fra Vatlestraumen etter 7 timer (modelltid). Strømretningen er sørlig, og det er brukt konstant viskositet i hele modellområdet på hver av kjøringene.
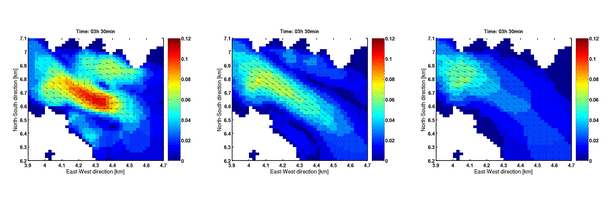
Figurene over viser dermed at mengden viskositet som blir brukt i numeriske modeller påvirker resultatet i vesentlig grad, og et fornuftig valg av denne størrelsen er viktig for å få troverdige resultater.

Like nord for Vatlestraumen ligger det en liten holme som heter Trollholmen. Modellresultatene viser at Trollholmen kan ha et interessant strømbilde i sundet inn mot fastlandet. Modellen predikerer at strømmen gjennom sundet for det meste er rettet sørover selv om tidevannstrømmen gjennom Vatlestraumen er nordlig. Det viser seg at en virvel dannes på nordsiden av holmen, se figur, og at denne virvelen sørger for den sørgående strømmen. I en tidevannsperiode på rundt 24 timer er strømmen rettet sørover i ca 20 timer. I de resterende ca 4 timene er strømmen svak og rettet nordover. Dette skjer når tidevannstrømmen gjennom Vatlestraumen snur og går mot nord. I dette området er det visstnok en strøm som heter Minnestraumen. Det kunne vært interessant å sammenlikne modellresultatene med målinger av Minnestrømmen i dette området.

Steinsundet deles av Vestre Steinsundholmen som er en relativ stor øy som ligger på vestsiden av Bjorøyna med Austre Steinsundholmen tett ved. Mellom Bjorøyna og Steinsundholmen går Steinsundet eller det Sørlige Steinsundet. Dette er et ganske trangt sund som er rundt 10 m dypt. Nord for Steinsundholmen, midt i det nordlige Steinsundet, ligger Kjerringholmen. Sørvest for Kjerringholmen ligger en grunne, og denne grunnen og Kjerringholmen styrer mesteparten av strømforholdene i det Nordlige Strømsundet. Når sørgående tidevannstrøm avtar viser modellresultatene at man kan finne to virvler i det Nordlige Stramsundet. Den ene er lokalisert nordvest for Steinsundsholmen og den andre som er en del svakere er plassert nært grunnen sørvest for Kjerringholmen. Strømretningen i det Nordlige Steinsundet er sørover, mens i det Sørlige Steinsundet er strømretningen allerede dreiet nordover.
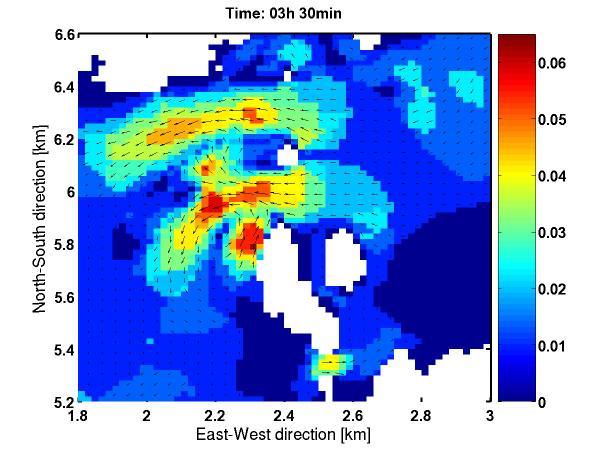
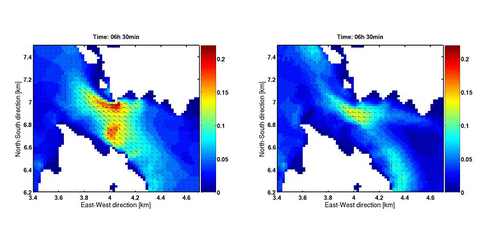
Den dybdemidlede maksimalhastigheten blir for det meste redusert, men i områder med sterk fokusering kan den også øke. Virvlene blir for det meste svekket når sjiktning er til stede. Dette skyldes nok dels at hovedstrømmen blir mer fokusert og gjerne redusert i tillegg, noe som gjør at medrivningen blir mindre, og dels at det blir vanskeligere å danne barotrope virvler inn mot grunnere områder på grunn av sjiktningen.

På grunn av at strømmen ved tetthetssjiktning blir mer fokusert over dypere områder endres strømstyrken i det Nordlige Steinsundet. I sundet sør for Kjerringholmen øker hastigheten mens i sundet nord for Kjerringholmen blir den redusert. Den nordgående strømmen i det Sørlige Steinsundet blir kraftig styrket. Transporten over grunnen vest for Kjerringholmen som i den barotrope simuleringen var påtagende er nesten ikke tilstede i simuleringen med sjiktning.

Både i Helle sin rapport og i Kystverket sin rapport for "Rocknes"-ulykken beskrives det at strømretningen kan skifte med dypet. Dette finner en også i modellen med sjiktning. Et eksempel fra et nord-sør snitt tatt på det smaleste over Vatlestraumen er vist i figuren under.
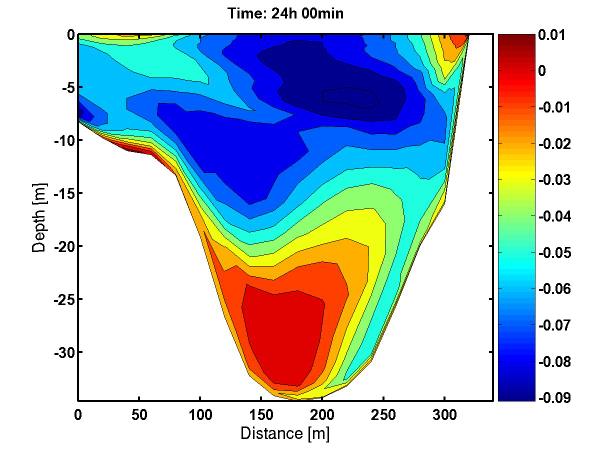
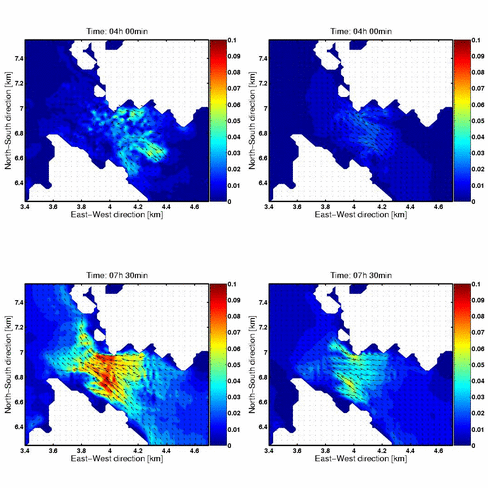
Figurene etter 4 timer viser at virvler er lokalisert i omtrent samme område. Det er to hovedvirvler tilstede i simuleringene, og disse er lokalisert i rett øst for den trangeste passasjen i Vatlestraumen. Her er det en nordlig virvel som roterer i positiv retning, og en sørlig virvel som roterer i negativ retning. Størrelsen på virvlene er større og glattere og strekker seg mer østover i simuleringen med BOM i forhold til simuleringen med MIT. Styrken på virvlene er kraftigere i BOM. Begge modeller gir svake strømmer langs Gavlen som er det nordligste punktet på Bjorøyna. Denne strømmen strekker seg sørover langs vestsiden av Bjorøyna. Nordover for Vatlestraumen viser BOM en svak, jevn homogen strøm. Denne er også tilstede i nærheten av Trollholmen i MIT kjøringen, men her er den mer oppstykket.
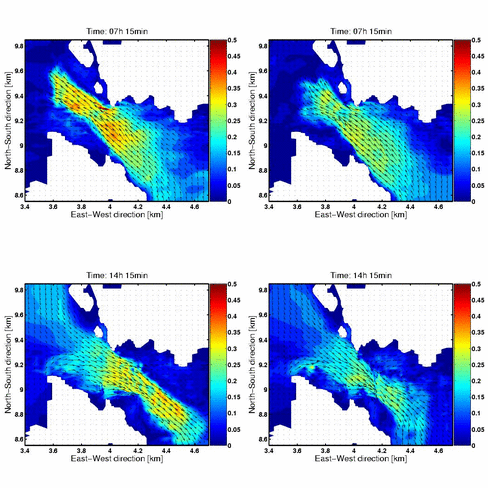
Etter 7 1/2 timer er tidevannsstrømmen rettet nordover i modellene. Begge modellene gir en intensifisering av strømmen over grunnene der Revatangen lykt og Minnestraumen lykt er plassert. Dette er på det smaleste av Vatlestraumen, og her er det en renne som har en tendens til å styre strømmen. I resultatene fra MIT koden ser en at strømmen blir spredd på vei nordover etter å ha passert den smaleste delen av Vatlestraumen og at en hoveddel går nordover mot Håkonshella. I BOM simuleringen formes en relativ smal jet som er rettet inn mot dypere vann i det samme området og spredningen av strømmen er liten. Også i disse figurene ser man at BOM gir glattere resulterer.
Det som kanskje er mest påfallende er likevel de store forskjellene i strømmønster og strømretning når det er sterk tidevannstrøm gjennom Vatlestraumen. Mens BOM ser ut til å ha en tendens til å fokusere strømmen mot dypere vann, er det nesten det motsatte som skjer i MITgcm, der hovedstrømmen blir spredd utover og kan gå mot grunnere vann.
Hastighetene er forskjellige i simuleringene. Hastighetene er generelt omtrent dobbelt så store i resultatene fra BOM. Dette henger nok sammen med at BOM har glattere bunntopografi og derfor bremser strømningen mindre enn hva som er tilfellet i MITgcm. Viskositetene påvirker også hastighetene i modellkjøringene. I BOM og MIT er viskositetene forskjellige, og dette vil naturligvis også påvirke modellresultatet.
Kunnskap om oppbygning og numeriske egenskaper for modellen er i mange tilfeller uvurderlig. Løser egentlig modellen de matematiske likningene på en tilfredsstillende måte?
Et viktig poeng er at en modell aldri kan gi et godt svar hvis geometri, drivkrefter og initialverdier ikke har god nok nøyaktighet. For å oppnå realisme og ha evne til prediksjon er man altså sjanseløs uten gode måledata. Og hva er gode måledata?
En annen svært viktig modelleringsaktivitet er validering. Vi trenger selvfølgelig også måledata for i det hele tatt å vite om vi har evne til prediksjon. Noen hevder numerisk modellering av sjøen er meningsløst uten bruk av høykvalitets måledata - ved å endre parametere i modellen innen en forventet naturlig variasjon vil den kunne gi "hva som helst" som svar. Argumentet går i at nytteverdien av numeriske modeller kun ligger i det å fylle i hullene i måledata.
Hvis hovedmålet med modelleringen ikke er prediksjon, men å øke forståelsen for fysiske prosesser er ikke måledata like kritisk. Man kan komme langt ved å bruke idealiserte drivkrefter som kvalitativt likner de reelle. Det er ofte hensiktsmessig å forenkle problem mest mulig for å forstå de grunnleggende elementene før en øker kompleksiteten. I denne rapporten har en variant av denne metoden blitt brukt, ved å vende hovedfokuset mot tidevannsdrevet strøm med og uten stratifisering gjennom den nordlige Raunefjorden. Vi har vist at vi med hjelp av enkle antagelser om randverdiene har kunnet reprodusere kvalitative beskrivelser av strømningsforholdene i området. Stratifiseringen som er brukt er beregnet fra måledata der målingene ble gjennomført våren 1974. Stratifiseringen brukt i modellen er videre idealisert, ved å anta at både temperaturen og saltholdigheten vil være lineære funksjoner med hensyn på dypet.
I den første tilnærmingen ble flere forenklinger gjort og mange viktige drivkrefter utelatt. Av forenklinger som ble gjort var å bruke en tidsforsinkelse på en halv time på tidevannet mellom nordlig og sørlig rand. Denne tidsforsinkelsen ble beregnet utifra hastigheten på en tidevannsbølge og bør bli sjekket ved målinger. Profiler for temperatur og saltholdighet ble beregnet fra (midlede) målinger fra mars måned, og her kan særlig sette spørsmålstegn til temperatur profilen som ser ut til å ha en mer S form enn en den lineære som er brukt i modellene. Når det gjelder målinger fra høsten, vil nok ihvertfall temperaturprofilen være en ganske annen enn for våren, da overflatetemperaturen gjerne er nærmere 15-16 grader Celsius enn de 4 gradene som ble brukt i modell kjøringene.
Dette studiet ble gjennomført med en forenklet dybdematrise. Det vil være viktig i videre studier å få tilgang til en enda mer nøyaktig bunntopografi. Dybdematrisen er interpolert fra navigasjonsdata, og vil dermed konsekvent være et underestimat for dypet i modellområdet.
Av drivkrefter som er utelatt kan en nevne den Norske Kyststrømmens styrke og dens påvirkning av strømmønsteret i Raunefjorden og Vatlestraumen. Ferskvannsavrenningen fra Nordåsvannet som trolig vil påvirke strømningen gjennom Vatlestraumen, særlig på høsten da større nedbørsperioder opptrer og det øverste vannlaget kan bestå av hovedsakelig ferskvann. Den sannsynligvis største drivkraften som er utelatt er nok vind. Den lokale vinden vil i stor grad drive overflatestrømmen, mens vind fra større lavtrykk vil være med å flytte vannmasser til eller fra kysten, og dermed påvirke både sjiktning og vannstand.
Vi tror at de to modellene som er satt opp er et godt utgangspunkt for videre arbeid med modellvalidering i området, og de vil også være godt egnet til eksperimentering med forbedrede drivkrefter i studentoppgaver på hovedfags eller doktorgradsnivå.